Sumar vectores significa juntar dos o más vectores para obtener como resultado uno nuevo.
La suma de vectores encuentra su aplicación en la física, mecánica y otras áreas, donde los vectores se utilizan para representar alguna magnitud como velocidad, desplazamiento, aceleración o fuerza.
Es necesario mencionar que un vector se escribe con letras mayúsculas y una flecha sobre ellos para indicar la dirección o con una letra en minúscula escrita en negrita. Los vectores se representan como la combinación de:
- Dirección: indica el ángulo que forma el vector con el eje de coordenadas “x”.
- Sentido: indica la dirección de la flecha del vector.
- Magnitud: es la longitud del vector y se denota encerrando en barras verticales las letras que lo denotan.
Por ejemplo; se tiene el vector (AB)→ la figura, donde A es el punto inicial (cabeza) y B es el punto terminal (cola), el cual también se puede denotar como u ((AB)→ = u) y su magnitud |(AB)→ | = 8 cm.

Por lo tanto, un vector tiene varias características que se utilizan al momento de realizar una suma entre dos o más vectores. Además, se emplean los componentes del vector que son sus proyecciones sobre los ejes cartesianos.
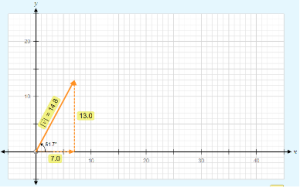
En el vector v → que se encuentra representado en el plano cartesiano, sus componentes son vx = 7, que significa que el vector tiene una magnitud de 7 unidades en el “eje x”, y la magnitud del vector en el “eje y” es vy = 13.
La longitud del vector es |v →|=14,8, la cual fue hallada usando el teorema de Pitágoras:
|v → |= v = √(〖vx2+〖vy〗2) → v = √(132+72) ≈ 14,8
Suma de vectores conocidos sus componentes
Si se desea sumar dos vectores A→ y B →, conocidos los componentes de ambos vectores,
A→ = (ax,ay) y B→ = (bx,by )
Se puede calcular la suma como:
A→ +B→ = (ax,ay )+(bx,by ) = (ax+bx,ay+by)
Se define la suma de vectores A→ y B → , como el vector resultante de sumar las coordenadas semejantes de los vectores dados.
De igual manera, si se agrega una tercera coordenada, es decir; los ejes “x, y, z”; los vectores se encuentran en el plano tridimensional, la suma A→ y B → y , donde:
A →= (ax,ay,az) y B →= (bx,by,bz)
A→+B →= (ax,ay,az) +(bx,by,bz) = (ax,+bx, ay+by, az+bz)
Si se tienen más de dos vectores, el procedimiento es el mismo, dependiendo de sus componentes.
Para entender el procedimiento de suma de vectores en función de sus componentes, se realiza la suma del vector A→= (4,1) y B → = (2,6). Aplicando la fórmula se tiene:
A→+B →= (4,1)+(2,6) = (4+2,1+6) = (6,7)→A→+B → = (6,7)
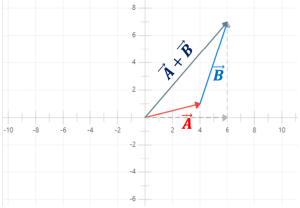
Los componentes finales del vector resultante (A→+B →) son 6 unidades en el “eje x” y 7 unidades en el “eje y”. Se puede hallar su magnitud donde:
|A→+B →| = √(62+72) = √(36+49) = √85 ≈ 9,21 unidades
Suma de vectores conocida la magnitud y el ángulo
Si se conoce la magnitud del vector y el ángulo que forma con el “eje x”, se pueden hallar los componentes rectangulares de dicho vector.
Entonces, para encontrar la suma de dos o más vectores conocidos su magnitud y ángulos, se deben seguir los siguientes pasos:
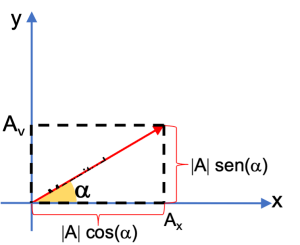
- Hallar las componentes de cada vector: para esto se utilizan las razones trigonométricas
- Fórmula para hallar el componente en “y”: Ay = A * sen(α)
- Fórmula para hallar el componente en “x”: Ax = A * cos(α)
- Calcular las componentes del vector suma: que se hace sumando los componentes encontrados de los vectores a sumar, según se explicó en el apartado anterior.
- Calcular la magnitud y el ángulo del vector resultante: con los componentes del vector resultante se realizan los cálculos.
Para el vector resultante C→ de componentes C→ la magnitud es:
v = √(Cx2+Cy2 )
y el ángulo de C→ es la tangente inversa de sus componentes:
ángulo C = tan-1 (Cy/Cx )
Para aplicar las fórmulas conocidas, se realiza el siguiente ejemplo. Sean los vectores P→ de magnitud 8 Newton y ángulo 25° y el vector Q→ = 9N, 68°. Hallar el vector suma S→.
Paso 1. Encontrar las componentes de cada vector.
- Para el P→
Px= P * cos(α) = 8 * cos(25) = 7.25
Py= P * sen(α) = 8 * sen(25) = 3.38 - Para el Q→
Qx = Q * cos(α) = 9 * cos(68) = 3.37
Qy = Q* sen(α) = 9 * sen(68) = 8.34
Paso 2. Hallar la suma: S→ = P→ + Q→ = (7.25+3.37,3.38+8.34) = (10.62 ,11.72)
Paso 3. Calcular la magnitud del vector resultante:
S→ = √((10.62)2+(11.72)2) = √(112.78+137.36) = √(250.14) = 15.81N
El ángulo del vector es:
ángulo S = tan-1 ((11.72)/(10.62)) = 47.82°
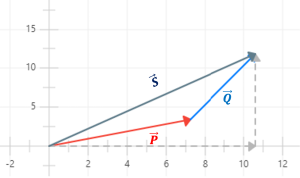
Componentes: S→ = (10.62 ,11.72)
Magnitud: |S→| = 15.81N
Ángulo: ángulo S = 47.82°