La velocidad angular es una medida de la rapidez con la que un objeto gira alrededor de un eje o punto.
La velocidad angular es una de las magnitudes fundamentales en el estudio de la física. También se conoce como velocidad de rotación y vector de frecuencia angular.
Generalmente, se denota con la letra griega ω (omega), aunque algunas veces también utilizan (Ω).
Si un objeto se desplaza en una trayectoria circular, se dice que la frecuencia o la velocidad angular es la cantidad de rotaciones, ciclos o vueltas que el objeto completa en un tiempo específico.
En la figura se representa el movimiento circular de un objeto que se mueve del punto A al B, en t segundos, de modo que el radio OA barre un ángulo θ al mismo tiempo.
A medida que el objeto se mueve alrededor de la trayectoria circular y pasa a través de ángulo θ, este se mueve con una velocidad angular ω.
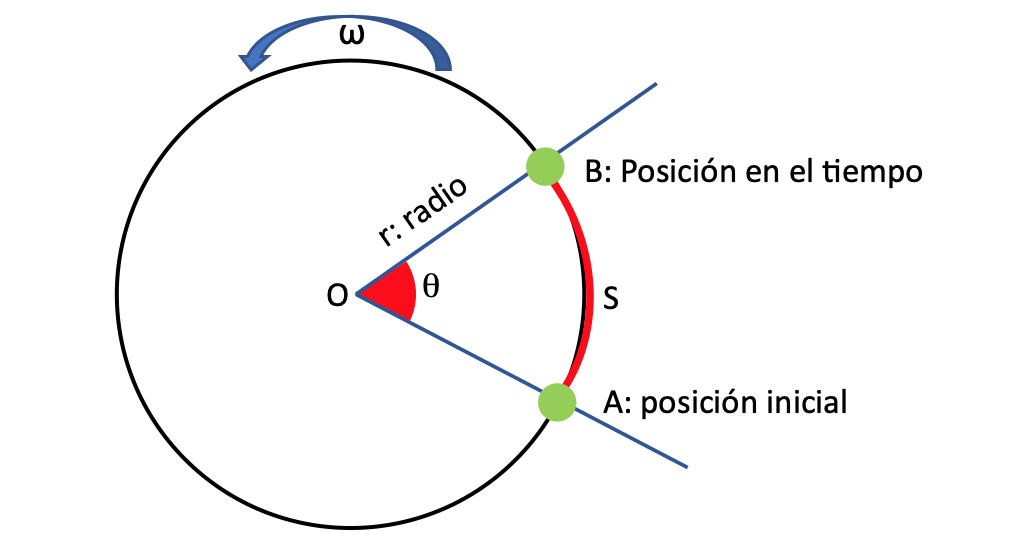
La velocidad angular se mide en ángulo por unidad de tiempo; por lo tanto, la unidad en el SI de la velocidad angular es radianes por segundo (rad/s).
Fórmula de la velocidad angular y sus variables
La velocidad angular se puede calcular de diferentes maneras según las variables de entrada parámetros
A. Velocidad angular en función del ángulo de giro y el tiempo
La fórmula de la velocidad angular en función del ángulo de giro y el tiempo viene dada por:
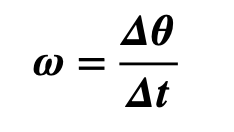
Donde:
- La velocidad angular es (ω), medida en radianes sobre segundo (rad/s).
- La variación del ángulo de giro es (Δθ), medido en radianes.
- El intervalo de tiempo transcurrido (Δt), medido en segundos.
Es necesario mencionar que cuando la velocidad angular es positiva indica una rotación del objeto en sentido contrario a las agujas del reloj.
En cambio, al ser (ω) negativa el cuerpo se desplaza en el sentido de las agujas del reloj.
Ejemplo: Un ciclista está dando vueltas en una pista circular con un ángulo de giro de 6,28 rad. El ciclista tarda 30 segundos en dar una vuelta completa al velódromo. Se desea conocer la velocidad angular promedio del ciclista.
Solución: Utilizando la ecuación conocida: ![]() y sustituyendo los valores conocidos se obtiene:
y sustituyendo los valores conocidos se obtiene:
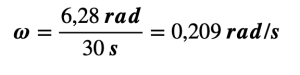
Por lo tanto, la velocidad angular promedio del ciclista es de aproximadamente 0.2094 radianes por segundo.
B. Velocidad angular en función de la frecuencia
Otra manera de hallar la velocidad angular es conocida la frecuencia.
![]()
Donde:
- ω: es la velocidad angular en radianes por segundo
- f: la frecuencia en Hertz
- π: es la constante matemática pi (aproximadamente 3,1416).
La relación entre la frecuencia angular y la velocidad angular es similar a la que existe entre la rapidez y la velocidad.
La frecuencia angular es una magnitud escalar mientras que la velocidad angular es un vector pseudo.
Ejemplo: Se tiene una lavadora cuya frecuencia de rotación del tambor es de 20 Hz. ¿Cuál es la velocidad angular con la que gira el tambor?
Solución: Si la frecuencia es![]() , se tiene que:
, se tiene que:

C. Velocidad angular en función de la velocidad lineal y el radio
La velocidad angular y la velocidad lineal están relacionadas a través del radio de la trayectoria circular.
Un cambio en la velocidad angular afectará directamente la velocidad lineal del objeto, y viceversa.
Por esto, se puede derivar otra fórmula de velocidad angular a partir de la relación de la velocidad lineal y el radio utilizando el producto vectorial, que es:
![]()
Al reescribir la ecuación se obtiene que:
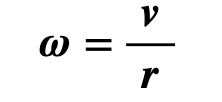
Donde:
- ω: es la velocidad angular en rad/s
- v: es la velocidad lineal en metros por segundo
- r: es el radio de la circunferencia en metros.
Esta fórmula indica que la velocidad angular es inversamente proporcional al radio de la trayectoria circular. Es decir, cuanto mayor sea el radio, menor será la velocidad angular y viceversa.
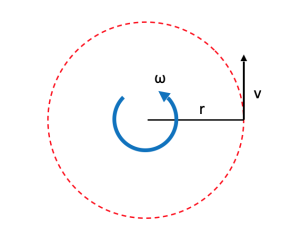
Ejemplo: Una bicicleta tiene una rueda de 0.5 metros de radio. Si la bicicleta avanza a una velocidad de 5 m/s, ¿cuál es su velocidad angular?
Solución: Se puede calcular la velocidad angular utilizando la fórmula ![]()
Despejando ω:
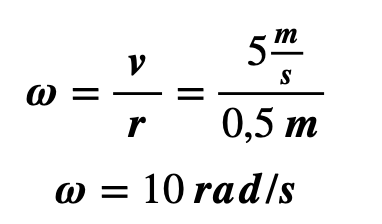
Por lo tanto, la velocidad angular de la rueda de la bicicleta es de 10 rad/s.
Por qué se estudia la velocidad angular
- El concepto de velocidad angular es fundamental para describir y entender el movimiento circular en la física y otras áreas de la ciencia y la ingeniería.
- Permite describir el movimiento circular de los objetos y sistemas, como las ruedas, los engranajes, las turbinas y los planetas.
- También es importante porque está relacionada con otras cantidades físicas, como la velocidad lineal, la aceleración angular, la aceleración lineal y la fuerza.