El péndulo simple es un concepto fundamental en física que describe el comportamiento de un objeto suspendido de un punto fijo, que oscila hacia adelante y hacia atrás en torno a una posición de equilibrio estable.
Esta forma de movimiento es ampliamente observable en situaciones cotidianas, como un columpio en un parque infantil o el péndulo de un reloj de pared.
Este tipo de movimiento se define como el movimiento de vaivén de un péndulo de forma periódica, y el punto central de oscilación se conoce como posición de equilibrio.
Se produce en un plano vertical y es impulsado principalmente por la fuerza gravitacional de la Tierra.
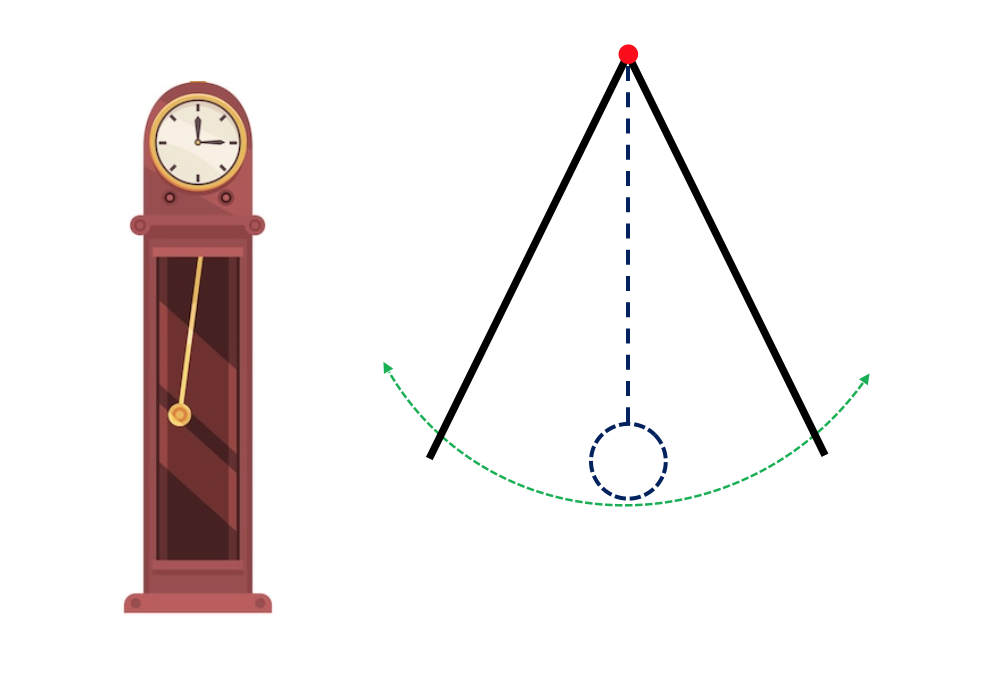
El movimiento de péndulo simple es un ejemplo clásico de movimiento oscilatorio que se produce cuando un objeto se suspende de un punto fijo y oscila hacia adelante y hacia atrás bajo la influencia de la gravedad.
¿Qué es el Péndulo Simple?
El péndulo simple es un sistema físico compuesto por una masa puntual (m) suspendida de un punto fijo (punto de pivote P) mediante un hilo o cuerda de longitud (L) inextensible y sin masa.
La partícula suspendida se le conoce como “el bob del péndulo”.
El punto de suspensión es esencial en esta configuración, ya que sirve como punto de referencia desde el cual el péndulo realiza sus movimientos oscilatorios.
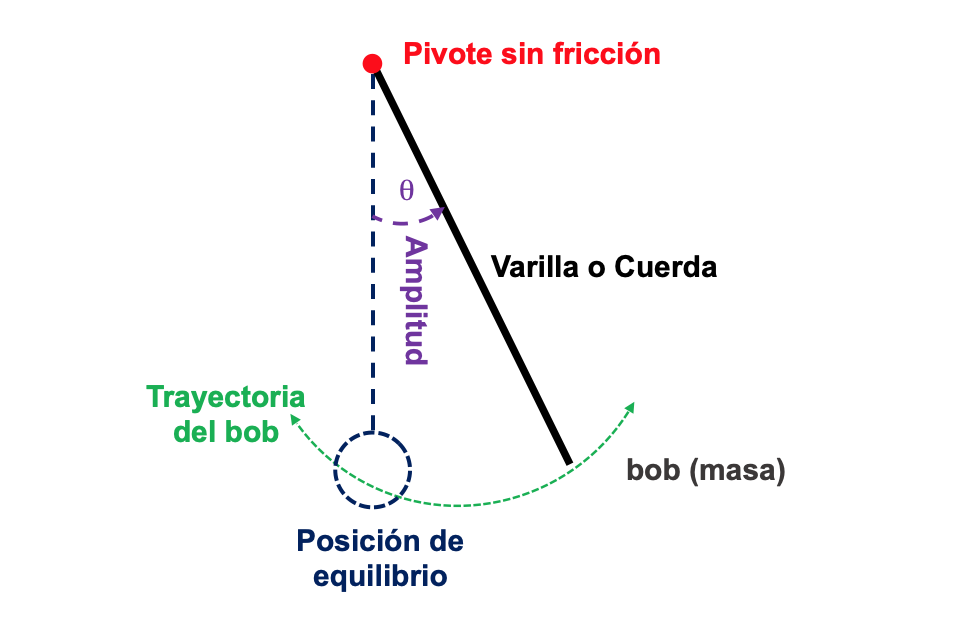
Características del Movimiento de Péndulo Simple
El movimiento de péndulo simple exhibe varias características distintivas que lo hacen un objeto de estudio relevante en la física:
- El movimiento del péndulo simple es periódico y oscilatorio.
- El movimiento se lleva a cabo en un plano vertical.
- La oscilación se produce a lo largo de una línea recta en este plano, y el péndulo se mueve hacia adelante y hacia atrás en una trayectoria curva.
- El péndulo simple cuelga verticalmente en su posición de equilibrio, donde la cuerda se encuentra en posición vertical y la masa no está desplazada en ningún sentido.
- En este tipo de movimiento se considera la fricción insignificante entre el aire y el sistema.
- El brazo del péndulo no se dobla ni se comprime y no tiene masa.
- El péndulo oscila en un plano perfecto.
- El periodo del péndulo no depende ni de la masa del péndulo, ni de la amplitud del movimiento.
Fórmulas del Movimiento de Péndulo Simple
En el movimiento del péndulo simple, se utilizan varias fórmulas importantes para describir y analizar su comportamiento.
A continuación, se presentan las fórmulas más fundamentales:
Fórmula del período (T)
El período del péndulo (T) es el tiempo que tarda en completar un ciclo completo de oscilación, es decir, desde su punto más alejado a la izquierda, pasando por la posición de equilibrio, hasta su punto más alejado a la derecha y de vuelta a la posición de equilibrio.
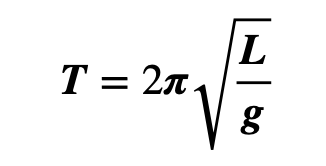
Donde:
- T: es el período (en segundos).
- L: es la longitud de la cuerda o hilo (en metros).
- g: es la aceleración debida a la gravedad (aproximadamente 9.81 m/s² en la superficie de la Tierra).
Frecuencia de oscilación del Péndulo
La frecuencia es el número de ciclos completos que el péndulo realiza en un segundo. Se calcula como el inverso del período:
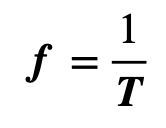
Donde:
- f: es la frecuencia (en hercios, Hz).
Ahora, para encontrar la frecuencia del péndulo como el recíproco del período se emplea la ecuación:
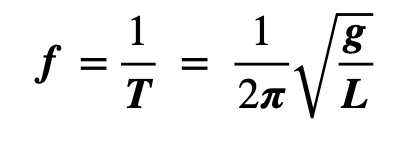
Longitud del péndulo
Para calcular la longitud de la cuerda (L), se puede reorganizar la fórmula inicial del periodo y se obtiene:
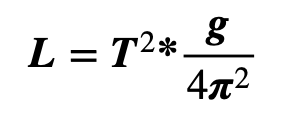
Aceleración debida a la gravedad
Se puede hallar (g) despejando esta variable de la ecuación original del periodo (T).
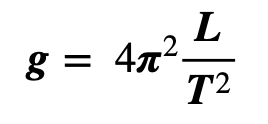
Ejercicios resueltos
Ejemplo 1. Se deseas construir un péndulo con un período de 1.85 segundos en la superficie de la Tierra, donde la aceleración debida a la gravedad es de aproximadamente ![]() ¿Cuál debería ser la longitud de la cuerda?
¿Cuál debería ser la longitud de la cuerda?
Solución: Los datos conocidos son:
T = 1,85 s
g = ![]()
L = ?
Se emplea la fórmula conocida de la longitud y se sustituyen los datos conocidos:
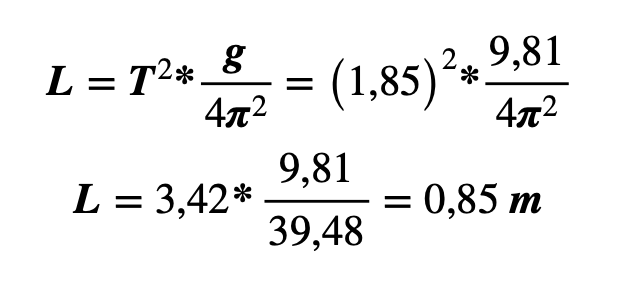
La longitud es de 0,85 metros.
Ejemplo 2. Hallar el periodo y la frecuencia de un péndulo simple que tiene una longitud de 0,72 metros, conociendo que g =![]()
Solución: Se tiene la siguiente información:
T = ?
f = ?
g = ![]()
L = 0,72 m
Se emplea la fórmula conocida de periodo (T):

Para la frecuencia:
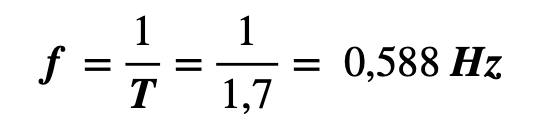
El periodo experimenta un periodo de oscilación de 1,7 segundo y una frecuencia de 0,588 Hz.