El concepto de un gas ideal es una simplificación teórica que se utiliza para facilitar el estudio y la comprensión de los gases en situaciones prácticas.
De allí, que la Ley de los Gases Ideales, estudia el comportamiento de las sustancias gaseosas en condiciones ideales, partiendo que se comportan de manera predecible y siguen una relación simple entre sus propiedades físicas, como:
Estas características se relacionan en una ecuación matemática simple, en función de las variables de: Presión (P), volumen (V), la cantidad de sustancia (n) y la temperatura (T).
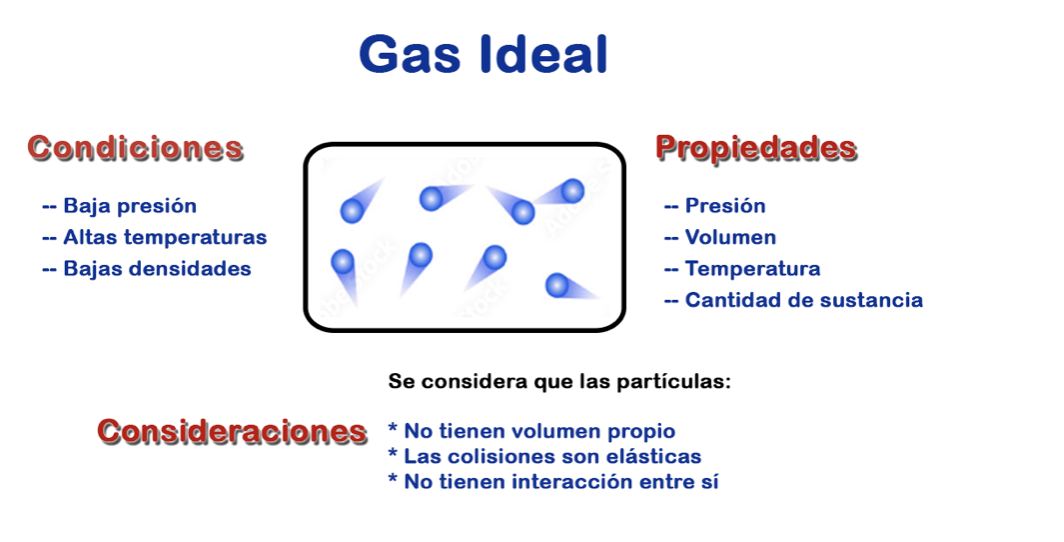
Es importante destacar que, en condiciones reales, ningún gas se comporta de manera completamente ideal.
En la realidad los gases ideales son un modelo hipotético considerado como una simplificación teórica que se utiliza para facilitar el estudio y la comprensión de los gases.
Sin embargo, la aproximación de un gas ideal es lo suficientemente precisa y útil para realizar cálculos prácticos.
Principios de la Ley de Gas Ideal
La Ley de los Gases Ideales es un principio que se desarrolló a lo largo del tiempo gracias a las contribuciones de varios científicos.
Aunque no hay un único descubridor, la formulación matemática final se atribuye principalmente al químico francés Émile Clapeyron, quien contribuyó a la ecuación de estado de un gas ideal al combinar las leyes de Boyle, Charles y Gay-Lussac en una sola ecuación.
Por esto, “Ley de los gases perfectos”, como también es conocida, tiene contribuciones significativas, derivándose de otras leyes como lo son:
- Ley de Robert Boyle
- Ley de Jacques Charles
- Ley de Joseph Louis Gay-Lussac
- Ley de Avogadro
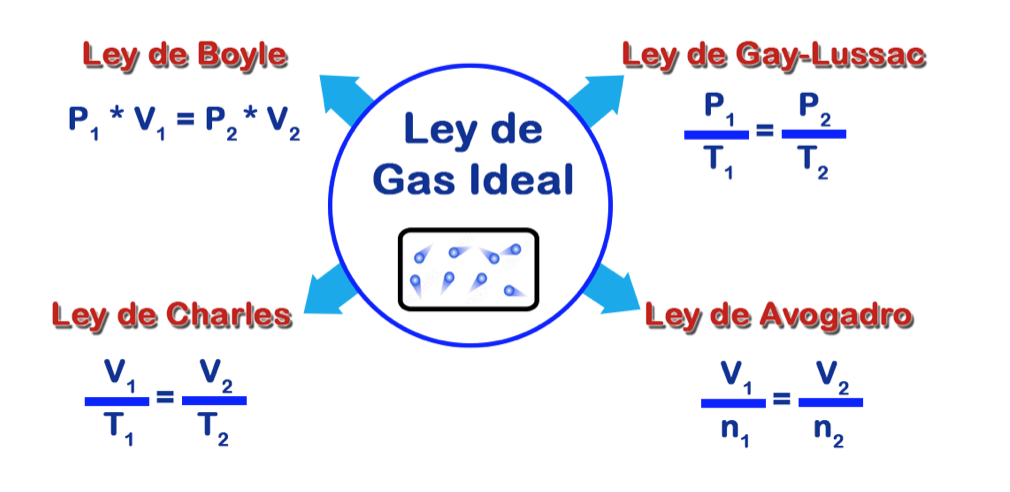
En conjunto, las investigaciones y contribuciones de estos científicos sentaron las bases para la formulación final de la Ley de los Gases Ideales.
Esta ley se utiliza ampliamente en la física y la química para describir el comportamiento de los gases en condiciones ideales.
Fórmula de la Ley de Gas Ideal
La fórmula de Ley de los Gases Ideales se expresa matemáticamente de la siguiente manera:
“El producto de la presión por el volumen en un gas, es igual a la cantidad de moles multiplicado por una constante llamada constante universal de los gases, y por la temperatura”.
Donde:
- P representa la presión.
- V es el volumen.
- n es la cantidad de sustancia en moles (mol). Es La relación entre la masa del gas (m) y su masa molar (M).
- T es la temperatura.
- R es la constante de los gases ideales. La constante física relaciona la energía cinética promedio de un gas ideal con la temperatura.
Unidades de ecuación de la Ley de gas ideal
Las unidades de medida para las variables en la ecuación son importantes para obtener resultados consistentes.
A continuación, se presentan las unidades de medida de las variables de la ecuación y algunas consideraciones sobre ellas.
- La presión (P): se mide en pascales (Pa), aunque también se usan atmosferas (atm) y milímetros de mercurio (mmHg) en algunas situaciones.
- El volumen (V): se expresa en metros cúbicos (m³), aunque en muchas aplicaciones, también se utilizan litros (L).
- La cantidad de sustancia (n) se mide en moles (mol), que es una cantidad fija de átomos o moléculas.
- La temperatura (T): se aconseja siempre medirla en kelvin (K), donde 0 K representa el cero absoluto (la temperatura más baja posible). Esto para evitar errores matemáticos, en el caso de hacer un cálculo que involucra una temperatura negativa o cero.
- La constante de los gases ideales (R): es la misma para cualquier tipo de gas y tiene un valor de aproximadamente 8,314 J/(mol·K), viene referido para la presión medida en pascales.
Otros valores de la constante R
- 0,08205746
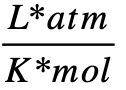
- 8,2057459×10-5
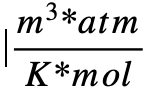
- 8,314472
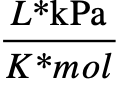
- 62,3637
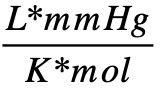
Ejemplos de aplicación de la Ley de gas ideal
Ejemplo 1: Un globo contiene 0,785 moles de N2 a 1,5 atm y a una temperatura 250K. ¿Cuál es el volumen del globo?
Solución: Se tiene la siguiente información:
- n = 0,785 moles
- P = 1,5 atm
- T = 250K
- R = 0,08205746
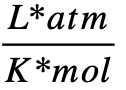(se utiliza este valor por conveniencia de unidades de medida).
Aplicando la ecuación estudiada, despejando la variable de volumen y sustituyendo los datos se tiene que:
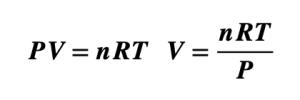
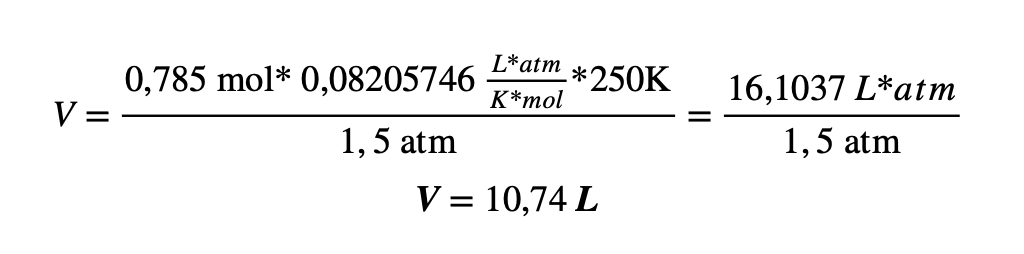
El volumen del globo es de 10,74 litros.
Ejemplo 2: Hallar la presión de un globo de helio que tiene un volumen de 5 litros a una temperatura de 25°C. Considere n = 4 mol
Solución: Se tiene la siguiente información:
- n = 4 moles
- V = 5 litros
- T = 25°C. convirtiendo a Kelvin: 25°C + 273.15 K = 298.15 K
- R = 8,314 J/(mol·K).
Aplicando la ecuación estudiada, despejando la variable de volumen y sustituyendo los datos se tiene que:
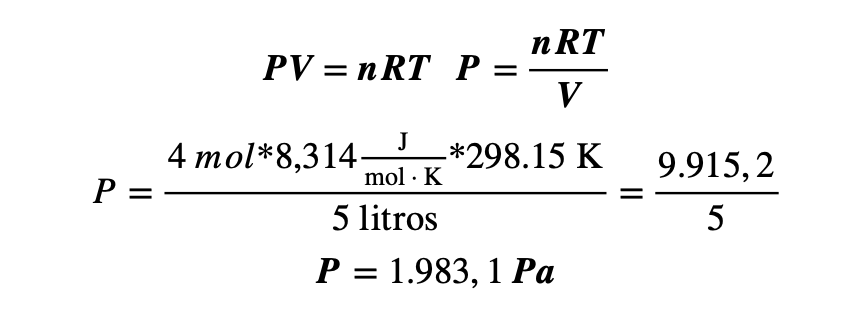
La presión del globo es de 1.083,1 Pa.